最近三年扎进了AI领域, 学了很多算法, 最近开始真正拉高维度看AI, AI不仅仅是Machine Learning, 还有State Based, Variable Bases, Logic编程等方法. 最近半年看了The book of Why, 深受启发, 看世界的角度也发生很大变化, 同时也觉得因果推理将是一个值得研究的好领域, 就算目前落地场景不多, 相信未来也是大有可为.
今天静下来, 好好看了在CausalNex库中, 用到的算法NOTEARS, 用于结构学习, 该论文发表在2018的NIPS, 方法神奇, 解决方案简洁, 以下是自己的一些笔记:
Paper: Zheng, Xun, et al. “DAGs with NO TEARS: Continuous optimization for structure learning.” Advances in Neural Information Processing Systems 31 (2018): 9472-9483.
1.主要问题
Bayesian Network Graph(DAG) Structure Estimating, 这是一个经典的NP-HARD问题
| 维度 | 传统解法 | NOTEARS |
|---|---|---|
| 思路 | combinatorial optimization problem, local heuristics for enforcing the acyclicity constraint, 例如 Order search, greedy search, … | Score based continuous learning, standard numerical algorithm |
| 复杂度 | O(d!), d is nodes | O(d^3), 当图入度很高时, 计算效率很高 |
| 优势 | – | 支持有向和无向图, 代码简洁不超过60lines, 与Global Optimization算法结果接近 |
| 局限 | 困难的组合优化问题 | 建模函数是Smooth function, nonconvex |
2.NOTEARS算法
其英文缩写是 Non-combinatorial Optimization via Trace Exponential and Augmented lagRangian for Structure learning
该算法我个人理解主要的贡献是找到一种数学建模方法, 把DAG的学习问题转化为可以用拉格朗日乘数法可求最优解的问题, 其建模的问题定义如下:

基于拉格朗日乘数法进行数值优化, 优势是:一个有n个变量与k个约束条件的最优化问题转换为一个解有n + k个变量的方程组的解的问题, 同时可复用一些优化算法: L-BFGS, quasi-Newton(PQN)
- 例如: 求f(x, y)在g(x, y)=c约数下的最大值, 可以转化为求下面函数的极值的问题:
- \(L(x, y, \gamma) = f(x, y) + \gamma * (g(x, y) - c)\)
下图是NOTEARS抽象为拉格朗日乘数的公式
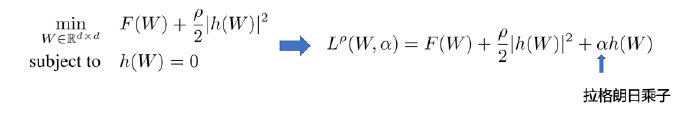
下图是NOTEARS的算法流程

3.NOTEARS算法效果
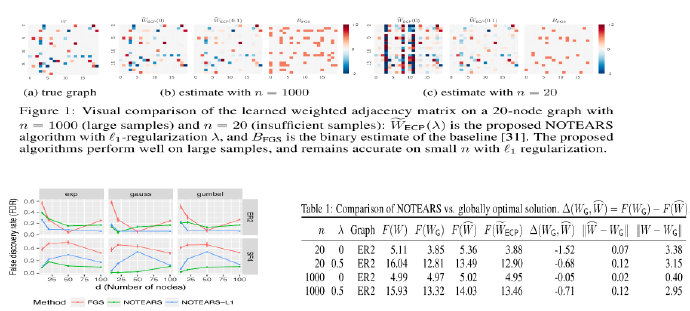
作者从ERS, SF4中生成了Node数为20, 样本量为1000和20的数据集, 图表示是邻接矩阵, 可看到学习后的效果和true graph很接近, 效果比Fast Greedy Search(FGS)要好, 同时和Global Optimizer的结果很接近, 准确性好
继续奋战, 下一波是Bayesian Network ^–^